Whiteboard: Somebody_s paper on the Ent last revised by 127.0.0.1 on May 25, 2007 11:25 am
Original Title: trees.tx
In this paper I will describe a data structure called the Ent. The Ent provides efficient access to large collections of interelated, evolving documents for groups of people working collaboratively. I will present it as a succession of progressively more powerful stages, each a simple modification of the preceding one. Several complicating factors will be ignored in the early going so the explanation can proceed in a coordinated fashion. Once the simple foundation has been presented, the gaps will be filled in.
The first version of the data structure supports reading large text documents. The succession of simple modifications will take us to one that supports complex editable multimedia structures. The final data base keeps track of modification history, allows users to look at any version, and displays the differences between documents. It also provides a permission system that allows users to control access to and modification of their work. The final form supports requests that make it possible for a user to find out when particular documents are modified or when annotations are added to them. All of this functionality is supported using algorithms that ensure that performance will continue to be good as the database grows, almost without bound.
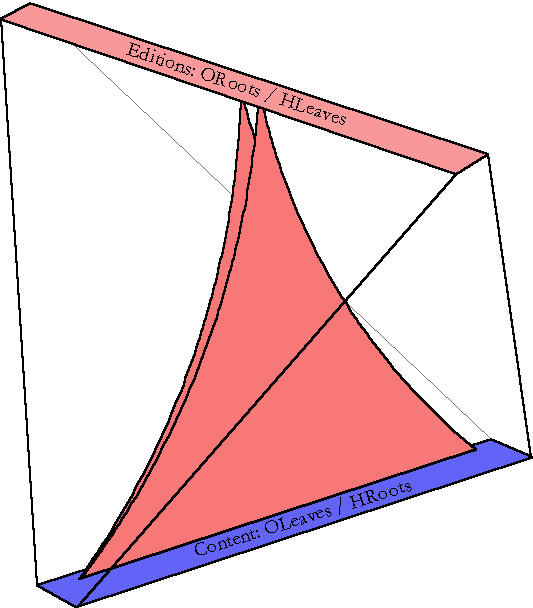
The final data structure is quite complex. The 5 color tetrahedron in figure 1 is an abstraction that shows all the major pieces and how they relate to one another. As I describe each part of the structure, I'll point back to this global view so you can stay oriented. Each of the pieces is always drawn in the same orientation and in the same color as in this global view.
missing figure 1
The presentation starts with simple balanced trees that provide access to ordinary text. In the first stage, the data structure is extremely simple, and only supports read access to unchanging text. We will add capabilities one at a time in stages of increasing sophistication.
In the second stage, we add the ability to edit the text indexed by the trees. Ordinary balanced trees are not efficient for data whose indices change. The change that enables editing is a modification to the representation of the nodes to store relative rather than absolute offsets of sub-nodes. This makes it possible for a change to one node at the root of a subtree to indicate movement of a large range of text. These editable trees are the ones represented in the global view by the upward-pointing red triangles.
In the third stage we make a second use of the relative coordinates. In addition to relocating a piece of data, the relative coordinates allow us to concisely indicate that a run of text appears in different places in different documents. The first use of this is in retaining the edit history of documents. Each time a document gets edited, we preserve the tree representing the old version, and construct a new tree that shares all the pieces that didn't change. The red tetrahedron in the global view represents a series of red triangles that have different roots and share some of their contents at the leaves.
The fourth incremental modification is to make the trees be doubly-linked so we can navigate from the leaves of the trees to their roots. With this change we can answer questions about which documents share contents. We draw these pointers toward the roots of documents in blue.
This modification gives us another set of trees that are upside-down with respect to the previous ones. We sometimes need to talk about both sets of trees at once, so we give directions in terms of rootward or leafward with respect to a particular tree, or use north and south when referring to global coordinates. Up and down might refer to either the global north/south, or to rootward and leafward in a particular tree so we'll avoid those terms.
In order to efficiently find the similarities between two given documents, we connect the internal nodes of the tree to navigation information (a canopy) stored outside the trees. This fifth addition to the design will allow us to follow a direct route from the contents of a variant document to the particular roots we're comparing. The navigation information is represented by the green south-pointing triangle on the right face of the tetrahedron.
The sixth and final modification will be another canopy that makes it possible to store recorders persistently. Recorders allow users to record queries about modifications to documents of interest. Storing this information within the volume of the ent would cost exponentially more.
Two key concepts are put off to the end of the presentation: handling data other than text, and keeping the trees balanced. The particular balancing algorithm we use is a variant of !Splay trees reference: Sleator & Tarjan ????. Splay trees provide amortized efficiency and also allow the indexing structure to adapt to changing patterns of access.
After I've presented the Ent as it applies to text, I'll explain our general concept of Coordinate Spaces. They give us the ability to apply the Ent to much more than text. The ent can represent the structure of multi-byte text, bitmaps of arbitrary dimensionality, sound, video, and more.
In an appendix, I'll describe the performance claims we make for this structure in detail and attempt to justify them. In general, access times grow with the log() of the content, and storage space grows at n log(n). Both are mostly unaffected by the number of edit changes or the amount of history that is kept. Changes can be stored in space and time proportional to the number of changes. Versions of a document can be compared in time proportional to the number of edits that changed one to the other, and with no intermediate storage growth.
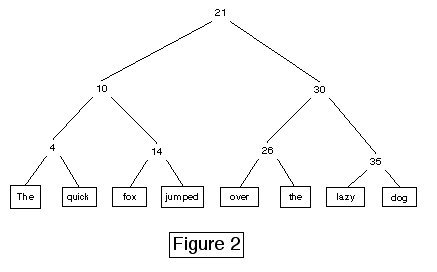
The basic data structure we start with is a simple binary tree. It only supports text retrieval. The tree is constructed from internal nodes called SplitLoafs?, which contain an integer (the split) and point to two child nodes. All the text before the position represented by the split is reachable through descendants of the left child; the right child accesses text after the split.
The text is stored at the leaves of the tree. To retrieve a range of text, start at the root of the tree and follow the branches that include any part of the range you're looking for. The tree walk is straightforward; a direct comparison with the split at any node tells which children you need to look at. To find the first character of the document, you would keep following left branches until you reached the leaves.

In the applications we want to support, documents constantly evolve. While the kinds of tree structures in common use throughout the industry can provide efficient access to stable data, they don't perform well if the indices have to be revised. In order to insert text in the previous structure, all of the nodes indexing text after the insertion would have to be relabeled to show their new addresses.
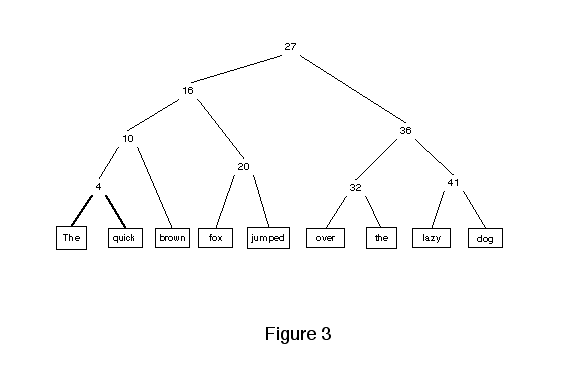
The first change to our balanced trees makes it possible to insert text without the need to change very much of the rest of the tree. A new type of node stores a displacement and has a single child. The displacement indicates the distance that descendants have been moved relative to the parent node.
The nodes that add offsets are called DspLoafs?. Dsp should suggest displacement, but allow you to continue to think clearly about them after we introduce non-integer coordinate spaces. The properties required of general dsps will be explained in the section on coordinate spaces.
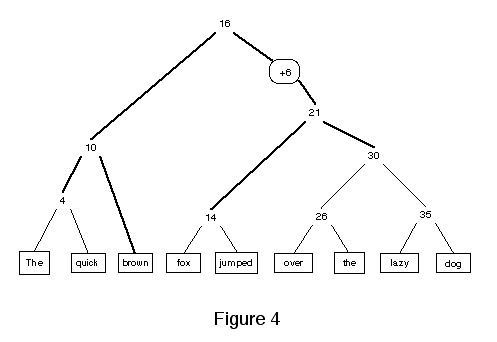
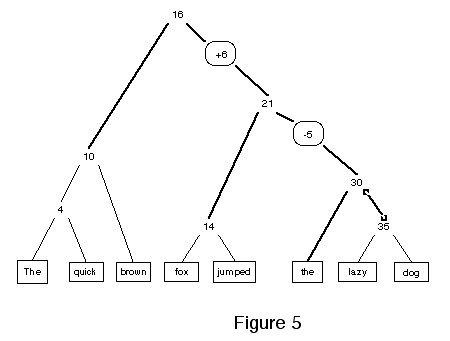
In figure 4 above, a new word is added in the middle of the sentence, and the changes are restricted to nodes on the path to the root of the tree. Insertions and deletions (see figure 5 below) always have this form. They affect a contiguous region of the data at the leaves, while the rest of the data structure can be fixed up without touching any nodes away from direct path to the root of the tree. The vasr us to have infinitely divisible spaces.
In the text version of the data structure, text is initially stored as complete runs. As pieces are copied with different sharing boundaries, the leafmost nodes subdivide themselves as necessary to represent the new chunks. The boundaries of chunks have no semantic significance, and aren't detectable from the external interface.
Rearrangements can always be performed with a combination of insertions and deletions, so the changes continue to be restricted to the path to the root of the tree from the boundaries of the changed regions. Trees are built (or re-used) to represent each of the chunks, and these trees are joined at their roots with Dsps that arrange them in the desired order.
When retrieving text, DspLoafs? modify the meaning of the location information found below them. When traversing toward the leaves of the tree, you accumulate dsps that you pass, and apply them to the splits as you encounter them.
The upward-pointing red triangular cross-sections of the Ent tetrahedron represent these trees with relative coordinates. When we want to include one of them as a small part of a much larger drawing, we use the red triangle as an icon.
missing figure 6a?
For example, a piece can be copied out of an edition so it can be shared. Rather than re-drawing the original triangle, it might be shown as figure 6b.
missing figure 6b?
The structures described so far provide all the tools necessary to retain the edit history of documents. The idea is simple: when making a change to a document you leave the tree representing the old version intact and accessible while re-using as much of the sub-structure as possible in building a new tree structure that represents the new version. The DspLoafs? that made it possible to re-use a piece of the tree in a different location also make it possible to use sub-trees in more than one tree at a time.
Here are the previous examples, re-drawn so that both the old and new versions can be read.
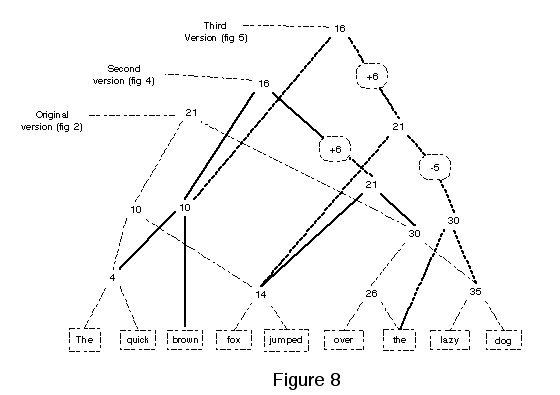
In the new picture, the parts drawn with solid lines are the original structure, and the dashed parts are new structure that represents a new state of the documen be navigated from its root in the same way as the trees from the first stage. The roots of the red forest represent different versions of documents.
The amount of additional space required by these structures grows slowly; whenever a new version shares most of its state with the previous one, it can cheaply re-use most of the old structure.
A simpler representation of editions that share data looks like a pile of triangles which are peeling away from one another at the top.
This is an abstraction of the idea that a new tree can share structure and data from older trees. The drawing exaggerates the thinness at the leafs to emphasize that there can be more sharing as you move in that direction.
This structure also supports the creation of new documents that share content in any way with others created previously. A new tree's superstructure can point to sub-structure that used to be part of unrelated documents. The sharing isn't detectably different from what happens when a new document is a revision of one other. This feature allows a new document to transclude (share/include) data from multiple preceding documents.
The data structure described so far stores multiple versions of documents, and describes how the parts have changed as the documents evolved to their present state. However, the structure records information that we can't extract efficiently: you could find out which editions contain a particular quoted fragment by walking to the leaves of every edition, but it would require traversing the entire data structure.
Doubly-linking the trees will allow us to efficiently answer questions about the multiple documents that transclude particular content. We'll be able to find all the sharers of a particular fragment of text, and where the fragment is within each of them. It's straightforward to navigate to the leaves of the red trees using the splits and Dsps to follow paths that include data of interest. Once there, following all north-going routes will reach all the editions that share some of the data. As you go, you subtract the Dsps to find where the text goes in the documents you've located.
As we consiters, we also consistently draw the reverse pointers in blue. The red pointers form trees we call the OTrees, because they describe the Organization of each edition.
The back-pointers form a complementary forest; its trees are called HTrees, since they represent the History of documents. They also represent the relationship between documents that share content because of copying.
When talking about what happens at individual nodes (often called histons) of the tree, we sometimes use paired chevrons as icons. This icon emphasizes the splits and the fact that the tree is binary, and ignores the Dsps.
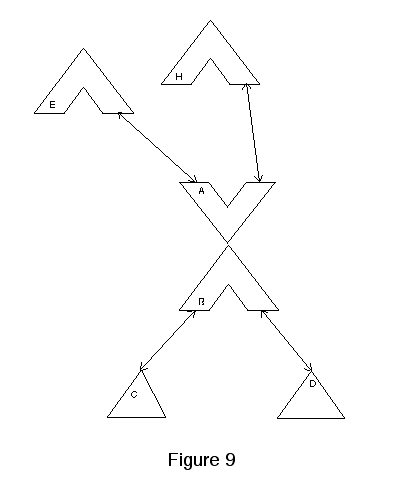
The histon in the center of figure 9 has two O-children. They contain its left and right descendants respectively. Its two H-Children represent editions that share its contents. This histon is on the right side of both of them, so they might be parts of different versions of a single document that contain this data in the same place.
Figure 9, while a useful abstraction doesn't show the way we actually represent the northward pointers. Rather than a binary tree of O-parents, we instead store a set of O-parents at each histon. The actual tree looks more like figure 10.
missing figure 10?
We will need to make a formal argument that the lack of a balanced tree in this direction won't hurt us, or else add the balanced tree of back-pointers. Neither of these has been done yet.
The blue HTrees correspond to the blue triangles in our global Ent tetrahedron. The tetrahedral shape arises because of the way we think about the two sets of trees interpenetrating. The red trees each start at a single root and "fan out in O," ("O" is the wide dimension of the leaves of an OTree?; it represents the contents of a document) while the blue trees "fan out in H." The ORoots? don't seem to line up neatly in a row until you look at it from the perspective of the data. From any run of text, all the sharers can be arranged linearly, so the picture is a clarifying representation. The roots of the HTrees are much easier to think of as being lined up and it's very useful to think of a dimension along which the H-Trees spread out. It's crucial to remember that H- anand inverted.
The sections below are much less complete than those above. I'm going to try to describe several alternative schemes that we might use to solve one final problem. The splits and dsps in the ent all give directions and locations relative to the data in various editions. They make it possible to traverse the tree southward to a particular leaf without making any false moves, or travel north and know the position of the data you started at when you reach an edition.
The corresponding traversals in the opposite directions are more problematic. There is neither an absolute nor a relative coordinate space description of all the editions and versions stored in the ent. This makes it difficult to have the "local roadsigns" that allow you to navigate directly to a particular edition starting from a particular piece of content. Even finding out whether a particular datum is contained in an edition seems to require a complete traversal of all the trees that point at the data.
What we want is to have some abstract equivalent to the dsps and splits that always give the location relative to the data, and which can be used to tell which children are relevant to a particular search.
The functionality we're looking for would allow us to label all the histons that are part of a particular edition inexpensively. That makes it possible to navigate from a particular datum directly to the edition, or to see immediately that it's not a part.
We've come up with a few different schemes to attack this problem. The first was called the DagWood?, and it involved the imposition of a tree ordering on all editions. The DagWood? works in concert with a canopy; more recent designs use canopies without the DagWood?. Canopies are "sideways" projections of the ent volume onto a single tree. A very recent proposal by Dean suggests storing endorsement information directly in the volume at every histon, and using that to navigate.
All of these schemes are intended to make it possible to start at the southern end of the ent, and navigate northward while rejecting paths quickly if they won't lead to a desired destination. If we can't do the quick rejection,sal of all of the sharers of the contents of the editions being compared.
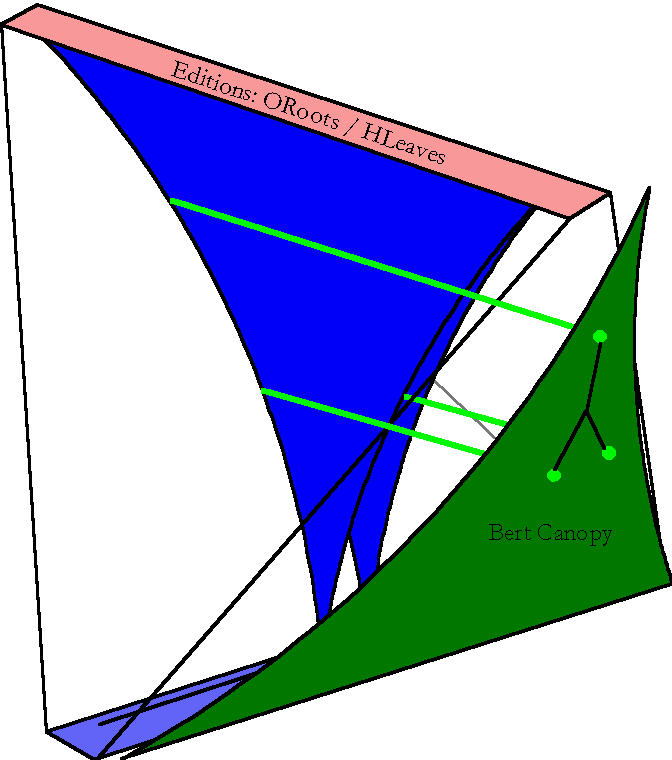
The Bert Canopy? is a separate tree structure outside the volume of the ent. It represents a sideways projection of the 3-d structure onto a metaphorical 2-d plane. Think of solid geometry, and a translucent tetrahedron lit from the side casting a shadow on a nearby wall, or of the trip-lets that Hofstadter used on the cover of Godel, Escher, Bach.

Note: only the sideways projections relate to Ents. The downward projection has no parallel to Ents.
The intent of this projection is to preserve information about distinctions between different versions and editions, and to collapse out information about data within an edition.
Each histon has a pointer to its canopy crum. There are no pointers back into the volume from the canopies, because many histons point to the same crum. The idea is to mark a path in the canopy that is visible from the histons. In order to navigate to a particular edition, you mark the path (in the canopy) from the crum for that edition to the canopy's root. Then at each histon, you look at each of the O-Parents and omit all that don't point to marked crums. As with the DagWood?, all you need in order for this to make the traversals tractable is that you reject false paths soon enough or often enough.
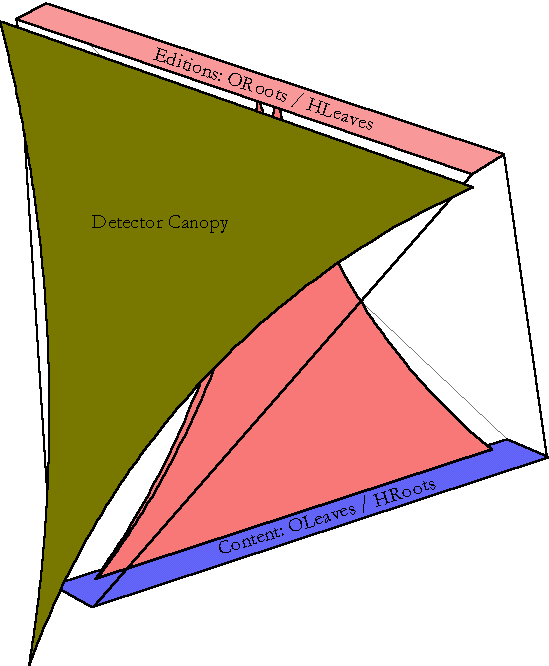
The Sensor Canopy? is used to store Recorders?. (They used to be called sensors, but were renamed when many people mis-heard censors.) It's a project along the other axis: it collapses out version and sharing information, and represents information about the structure of editions. Storing recorders in this projected tree provides a space savings:
Rather than storing a number of copies of (or pointers to) the recorder proportional to the complexity of the edition, it can be stored just once.
(this description is woefully inadequate. It's not worth more effort now)
In each canopy, there's a lot of leeway in building the tree. The only rule about relative locations of nodes is that reachability relations in the ent must be reflected in the canopies. If histon A has histon B as an ancestor or descendant in the O- and H-trees, then A's canopy crum must be reachable by traveling in the same direction (north or south) in the canopy. In order to maintain this invariant, histons that become shared by new editions have to point to more rootward crums. (I'm not going to explain in detail. Save it for a later pass.) This rootward migration of the pointers may reduce the discrimination that the canopies provide. We aren't sure how much it happens or how bad the problem is. This uncertainty has lead to several of the proposed revisions.
The current fallback position is that the rules for transitive reachability won't be applied across edition boundaries. The architects agree that this should solve the problem we're most worried about currently.
The recent proposal suggests that we could do better, at least in the insurance application, by storing a representation of the cumulative endorsements at every histon, and navigating northward by following all trails that match the set of endorsements on the ORoot? we want to reach. Recorders would also be stored within the ent itself.
This proposal seems to work because the endorsements provide a coordinate system which we can efficiently maintain in the ent volume. We expect to have few enough endorsements in the insurance application that the cost of maintaining the information throughout the volume won't give us trouble.
Recorders need to be reachable from the leaves of the OTrees so you can tell when some part of a document is linked-to or included in a new document. The canopy solution makes them reachable by storing them in the projected tree rather than in the volume. The new proposal suggests that we store them in the volume and migrate them upward in the tree to the frontier of the volume they apply to.
This is not enough detail that you should expect to understand, but when it gets explained later, you'll have heard it before.?